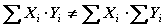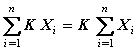1. Cifrado Vingenere
lunes, 12 de octubre de 2015
martes, 6 de octubre de 2015
martes, 29 de septiembre de 2015
sábado, 26 de septiembre de 2015
Practica 5
1.- Programa recursivo que suma n-numeros.

2.- Programa recursivo que suma n-numeros pares.
3.- Programa recursivo que invierte una palabra.

jueves, 24 de septiembre de 2015
Relación de recurrencia
En matemática, una relación de recurrencia es una ecuación que define una secuencia recursiva; cada término de la secuencia es definido como una función de términos anteriores.
An alisis de algoritmos recursivos
Cuando analizamos algoritmos recursivos es util describir la funci on de coste como una recurrencia.
Una recurrencia es una ecuaci on que describe una funci on en t erminos del propio valor de la funci on para argumentos m as cercanos a alg un caso b asico, para el que la funci on est a de nida expl citamente. Resolver una recurrencia signi ca encontrar la expresi on expl cita que de ne la funci on recurrente. Generalmente, nos bastar a con clasi car la funci on recurrente en una notaci on asint otica
Resoluci on de recurrencias mediante la t ecnica de expansi on
Ejemplo: Dada la recurrencia
De T(n/2)= T(n/2^2)+b obtenemos T(n)=T(n/2^2)+b+b
An alisis de algoritmos recursivos
Cuando analizamos algoritmos recursivos es util describir la funci on de coste como una recurrencia.
Una recurrencia es una ecuaci on que describe una funci on en t erminos del propio valor de la funci on para argumentos m as cercanos a alg un caso b asico, para el que la funci on est a de nida expl citamente. Resolver una recurrencia signi ca encontrar la expresi on expl cita que de ne la funci on recurrente. Generalmente, nos bastar a con clasi car la funci on recurrente en una notaci on asint otica
La recurrencia en la computación
La conexión con el análisis de algoritmos estriba en que la forma que se ha adoptado para medir las complejidades, utiliza funciones cuyo dominio son los números naturales, o en otras palabras, sucesiones. Si el algoritmo es recurrente, es de esperarse que las complejidades, como funciones que estiman la demanda de recursos a lo largo de la ejecución, sean sucesiones que satisfacen ciertas ecuaciones de recurrencia. En un algoritmo recursivo, la función t(n) que establece su complejidad viene dada por una ecuación de recurrencia. Una ecuación de recurrencia nos permiten indicar el tiempo de ejecución para los distintos casos del algoritmo recursivo (casos base y recursivo).Resoluci on de recurrencias mediante la t ecnica de expansi on
Ejemplo: Dada la recurrencia
De T(n/2)= T(n/2^2)+b obtenemos T(n)=T(n/2^2)+b+b
)
Repita la sustituci on correspondiente alguna vez m as, hasta que sea capaz de "adivinar" un expresi on patr on que generalice todas las sustituciones sucesivas.
T(n) =T(n/2^2) +b+b=T(n/2^3) +b+b+b=...=T(n/2^i) +ib
Supongamos que las raices son: r1,...,rk.
Entonces la soluci on de la recurrencia es de la forma:
Para encontrar los valores de las constantes c1,...,ck hay que establecerun sistema de ecuaciones con k casos particulares. Para las recurrencias no homogeneas, adem as aparece la ra i z b (de la parte derecha de la ecuaci on) con multiplicidad d+ 1 siendo del grado del polinomio p(n). Cuando hay una ra iz multiple rj, de multiplicidad m, entonces en la soluci on deben aparecer los sumandos siguientes:
miércoles, 23 de septiembre de 2015
Algoritmo recursivo a iterativo
Para explicar nuestro tema a tratar
utilizaremos la solución recursiva para el problema factorial:
1.- Analizar el algoritmo recursivo:
def facrec(n):
if (n==0):
return 1
else:
return n*facrec(n-1)
Ahora lo analizamos haciendo una
pequeña prueba de escritorio.
Si n=3:
def facrec(3):
if (3==0): #La condición es
falsa
#Ya que el if no se cumple no se cumple pasamos a
la siguiente condición
else:
return 3*facrec(2)
#Ahora la función fcrec() tiene un nuevo valor que es 2
def facrec(2):
if (2==0): #La condición es
falsa
#Ya que el if de nuevo no se cumple no se cumple
pasamos al else
else:
return 2*facrec(1)
# La función se volverá a
llamar hasta legar al caso base, que será hasta que se cumpla la condición
dentro del if
def facrec(1):
if (1==0): #La condición es
falsa
else:
return 1*facrec(0)
def facrec(0):
if (0==0): #La condición es verdadera
return 1
#Ya que la condición es
verdadera la función regresa un 1. Ahora mostrare lo que sucedería en cada
llamada a la función
def facrec(0):
return 1
def facrec(1):
return
1*1
=1
def facrec(2):
return 2*1
=2
def facrec(3):
return 3*2
=6
#Y asi podemos concluir que
3!= 6
2.- Decidir los
argumentos de la función que se llevaran acabo en variables.
En este ejemplo de factorial, los
resultados de el factorial se pueden guardar en una variable “total_factorial”
(acumulador) para la duración de cualquier iteración. En el ejemplo se muestra el
algoritmo factorial recursivo y la variable que se utilizara para el argumento
recursivo :
total_factorial=1
3.- Determinar la estructura del ciclo.
Podemos decir que las llamadas a la
función en un algoritmo recursivo son equivalentes a un ciclo, ahora solo
debemos decidir que estructura es mejor para resolver el algoritmo.
Por ejemplo el ciclo “Mientras que”,
funciona bien con iteraciones de una longitud determinada. Para otro tipo de
ciclos que tienen una duración estricta es conveniente utilizar las estructuras
“Para” (for) ó “Repite”(do_while).
En este caso seria conveniente utilizar
la estructuta “Mientras que” .
while()
4.- Determinar el fin del ciclo.
Por lo general el fin de una recursión
es cuando se cumple el caso base. En
este ejemplo de factorial, se sabe que
el factorial de un numero “n” se va a repetir n-1 veces (excepto el cero), por
lo tanto:
def factorial_iterativo(n):
total_factorial=1
i=1
while (i>=1):
total_factorial=total_factorial*i
i=i+1
return total_factorial
#El lenguaje que utilizo es python
#El lenguaje que utilizo es python
martes, 8 de septiembre de 2015
martes, 1 de septiembre de 2015
viernes, 28 de agosto de 2015
SUMATORIA
La sumatoria o sumatorio (llamada también notación sigma) es una operación matemática que se emplea para calcular la suma de muchos o infinitos sumandos.
La sumatoria o sumatorio se emplea para representar la suma de muchos o infinitos sumandos y se define como:

La expresión se lee: "sumatoria de Xi, donde i toma los valores de 1 a n".
La operación sumatoria se expresa con la letra griegra sigma mayúscula Σ.
i es el valor inical llamado límite inferior.
n es el valor final llamado líimite superior
Historia:
Gauss ha sido uno de los mejores matemáticos de todos los tiempos. Incluso se le ha denominado el “príncipe de las matemáticas”.

Su vida transcurrió a
lo largo de los siglos XVIII y XIX. Este matemático ya realizó grandes
proezas matemáticas desde que era un crío, como lo puede demostrar la
siguiente anécdota muy conocida:
La historia relata que cuando Carl Friedrich Gauss
tenía diez años su profesor de matemática le impuso al curso, como una
forma de mantenerlos ocupados por largo rato, el siguiente ejercicio:
Sumar todos los números desde el 1 hasta el 100, de este modo:
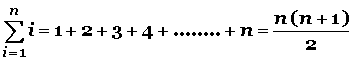
Si aplicamos la fórmula al problema anterior, tendremos:
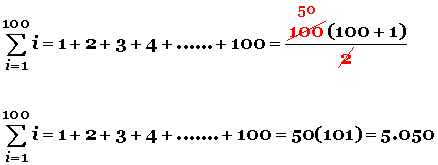
Por ejemplo, para sumar los primeros mil números naturales no tiene mucho sentido sumar número por número, si se puede usar la fórmula:
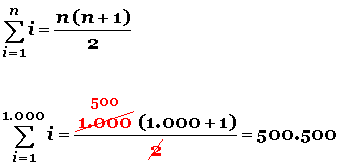
Sumar todos los números desde el 1 hasta el 100, de este modo:
1 + 2+ 3 + 4 + 5 + 6 + 7 + 8 + 9 + ……………….+ 98 + 99 + 100 =
Confiado en que los niños estarían ocupados durante
mucho rato, el profesor se enfrascó en sus tareas de estudio, pero a
los cinco minutos, el pequeño Gauss le entregó el resultado: 5.050.
Sorprendido, el profesor le pidió a Gauss que le explicara cómo lo hizo:
El pequeño se dio cuenta de que la suma del primer
número con el último (1 + 100 = 101) da un resultado que se repite
sumando todos los simétricos: 1 + 100 = 101; 2 + 99 = 101; 3 + 98 =
101; 4 + 97 = 101; etc., logrando establecer 50 sumas cuyo resultado es
101.
Entonces, hizo: 50 veces 101 es igual a 50 x 101 = 5.050
Este procedimiento nos conduce a la fórmula de la sumatoria de n números consecutivos:
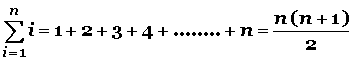
Si aplicamos la fórmula al problema anterior, tendremos:
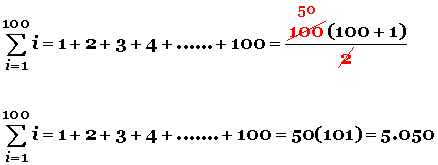
Por ejemplo, para sumar los primeros mil números naturales no tiene mucho sentido sumar número por número, si se puede usar la fórmula:
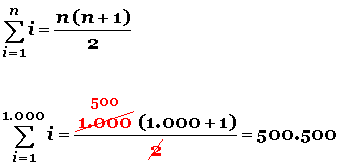
- Algunas fórmulas de la operación sumatoria:
Es frecuente el uso del operador sumatoria en Estadística.
La suma de las frecuencias absolutas se puede expresar como:
1. 

2. 

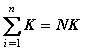
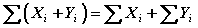
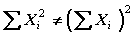

Y la media como:
1.

2.

Ejemplo:
En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones que muestra la tabla. Calcula la media.
| xi | fi | xi · fi | |
|---|---|---|---|
| [10, 20) | 15 | 1 | 15 |
| [20, 30) | 25 | 8 | 200 |
| [30,40) | 35 | 10 | 350 |
| [40, 50) | 45 | 9 | 405 |
| [50, 60 | 55 | 8 | 440 |
| [60,70) | 65 | 4 | 260 |
| [70, 80) | 75 | 2 | 150 |
| Σxi = 42 | Σxi · fi = 1 820 |

- Propiedades de la sumatoria
La suma del producto de una constante por una variable, es igual a k veces la sumatoria de la variable.
La sumatoria hasta N de una constante, es igual a N veces la constante.
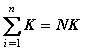
La sumatoria de una suma es igual a la suma de las sumatorias de cada término.
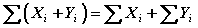
La sumatoria de un producto no es igual al producto de las sumatorias de cada término.
La sumatoria de los cuadrados de los valores de una variable no es igual a la sumatoria de la variable elevado al cuadrado.
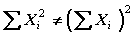
Referencias:
http://www.ditutor.com/estadistica/sumatoria.html
https://sferrerobravo.wordpress.com/2007/11/24/gauss-y-la-suma-de-los-n-primeros/
https://es.wikipedia.org/wiki/Sumatorio
http://www.profesorenlinea.cl/matematica/Sumatoria.html
miércoles, 26 de agosto de 2015
Practica 2
Programa 1: Programa que obtiene los dos mayores números de un conjunto de n-números

Programa 2: Programa que obtiene el mayor y la menor
diferencia de un conjunto de n-números
Programa 3: Programa que obtiene la media, moda y mediana de
un conjunto de n-números
Suscribirse a:
Entradas (Atom)