La sumatoria o sumatorio (llamada también notación sigma) es una operación matemática que se emplea para calcular la suma de muchos o infinitos sumandos.
La sumatoria o sumatorio se emplea para representar la suma de muchos o infinitos sumandos y se define como:

La expresión se lee: "sumatoria de Xi, donde i toma los valores de 1 a n".
La operación sumatoria se expresa con la letra griegra sigma mayúscula Σ.
i es el valor inical llamado límite inferior.
n es el valor final llamado líimite superior
Historia:
Gauss ha sido uno de los mejores matemáticos de todos los tiempos. Incluso se le ha denominado el “príncipe de las matemáticas”.

Su vida transcurrió a
lo largo de los siglos XVIII y XIX. Este matemático ya realizó grandes
proezas matemáticas desde que era un crío, como lo puede demostrar la
siguiente anécdota muy conocida:
La historia relata que cuando Carl Friedrich Gauss
tenía diez años su profesor de matemática le impuso al curso, como una
forma de mantenerlos ocupados por largo rato, el siguiente ejercicio:
Sumar todos los números desde el 1 hasta el 100, de este modo:
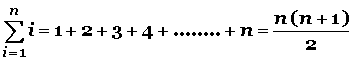
Si aplicamos la fórmula al problema anterior, tendremos:
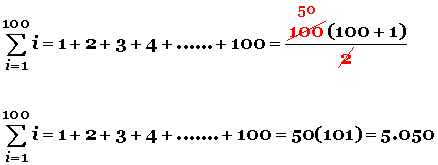
Por ejemplo, para sumar los primeros mil números naturales no tiene mucho sentido sumar número por número, si se puede usar la fórmula:
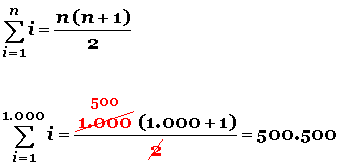
Sumar todos los números desde el 1 hasta el 100, de este modo:
1 + 2+ 3 + 4 + 5 + 6 + 7 + 8 + 9 + ……………….+ 98 + 99 + 100 =
Confiado en que los niños estarían ocupados durante
mucho rato, el profesor se enfrascó en sus tareas de estudio, pero a
los cinco minutos, el pequeño Gauss le entregó el resultado: 5.050.
Sorprendido, el profesor le pidió a Gauss que le explicara cómo lo hizo:
El pequeño se dio cuenta de que la suma del primer
número con el último (1 + 100 = 101) da un resultado que se repite
sumando todos los simétricos: 1 + 100 = 101; 2 + 99 = 101; 3 + 98 =
101; 4 + 97 = 101; etc., logrando establecer 50 sumas cuyo resultado es
101.
Entonces, hizo: 50 veces 101 es igual a 50 x 101 = 5.050
Este procedimiento nos conduce a la fórmula de la sumatoria de n números consecutivos:
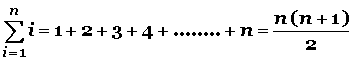
Si aplicamos la fórmula al problema anterior, tendremos:
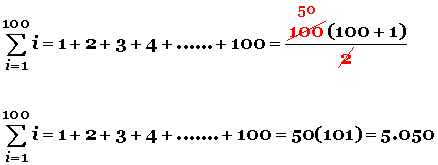
Por ejemplo, para sumar los primeros mil números naturales no tiene mucho sentido sumar número por número, si se puede usar la fórmula:
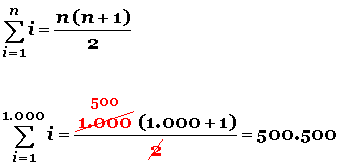
- Algunas fórmulas de la operación sumatoria:
Es frecuente el uso del operador sumatoria en Estadística.
La suma de las frecuencias absolutas se puede expresar como:
1. 

2. 

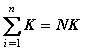
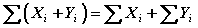
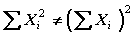

Y la media como:
1.

2.

Ejemplo:
En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones que muestra la tabla. Calcula la media.
| xi | fi | xi · fi | |
|---|---|---|---|
| [10, 20) | 15 | 1 | 15 |
| [20, 30) | 25 | 8 | 200 |
| [30,40) | 35 | 10 | 350 |
| [40, 50) | 45 | 9 | 405 |
| [50, 60 | 55 | 8 | 440 |
| [60,70) | 65 | 4 | 260 |
| [70, 80) | 75 | 2 | 150 |
| Σxi = 42 | Σxi · fi = 1 820 |

- Propiedades de la sumatoria
La suma del producto de una constante por una variable, es igual a k veces la sumatoria de la variable.
La sumatoria hasta N de una constante, es igual a N veces la constante.
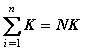
La sumatoria de una suma es igual a la suma de las sumatorias de cada término.
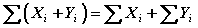
La sumatoria de un producto no es igual al producto de las sumatorias de cada término.
La sumatoria de los cuadrados de los valores de una variable no es igual a la sumatoria de la variable elevado al cuadrado.
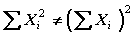
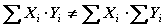
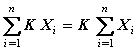
No hay comentarios:
Publicar un comentario